数学编程之阻尼效应

目录

• 目录
• 数学模型
  • 贝塞尔曲线
  • 编程模型之交互阻尼
• 回弹
  • 回弹模型
• 编程模型
  • 阻尼编程模型
  • 回弹编程模型
• 完整 demo 代码
• 参考文档

数学模型

在现实世界中，我们经常会看到各种阻尼效果：汽车轮胎的减震、拉开弹弓弹射、荡秋千逐渐到达最高点。在程序世界里，阻尼效应又被叫做“橡皮筋”效果，作为程序员肯定对这些场景不陌生：列表的的下拉刷新、拖拽触碰边界时的阻尼、以及炫酷的碰撞粒子回弹。

在物理学和工程学上，阻尼的力学模型一般是一个与振动速度大小成正比，与振动速度方向相反的力，该模型称为粘性（或黏性）阻尼模型，是工程中应用最广泛的阻尼模型。粘性阻尼可表示为以下式子：

$${\displaystyle \mathbf{F}=-c\mathbf{v}}$$

其中 F 表示阻尼力，v 表示振子的运动速度（矢量），c 是表示阻尼大小的常数，称为阻尼系数，国际单位制单位为牛顿·秒/米。

贝塞尔曲线

物体的阻尼运动，一定是随着时间的推移，其速率会越来越小，直到趋于 0。这种速率随着时间的变化，我们可以通过贝塞尔曲线来表达。

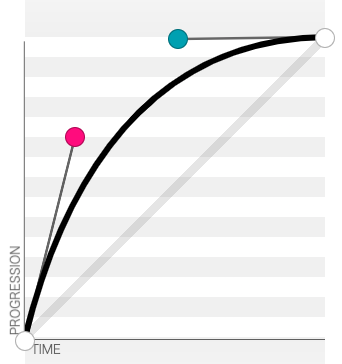
举一个简单的例子，我们希望一个 div 盒子能够遵循阻尼运动。

<div class="damping-box"></div>

.damping-box {
    position: relative;
    width: 100px;
    height: 100px;
    left: 200px;
    background-color: cadetblue;
    transition: left 2s cubic-bezier(.17,.67,.33,1);
}

.moving {
    left: 500px;
}

const box = document.querySelector('.damping-box');
setTimeout(() => {
    box.classList.add('moving');
}, 2000);

效果图如下，随着时间的推移，div 的运动速率逐渐减小，直到为 0。

在这里，我们使用了 css 里的 cubic-bezier 函数去模拟这个阻尼效果。

编程模型之交互阻尼

在实际的应用场景中，我们更多的是拖拽场景需要阻尼效果，比如下拉刷新，或者是上拉加载，这时候需要应用贝塞尔曲线建立起对应的编程模型。

以下拉刷新为例，我们来一步步建立起对应的编程模型。随着下拉距离的增加，下拉的阻力越来越大，速度越来越慢，直到最后速度为 0，下拉距离达到一个阈值。在这个过程中，我们可以抽象出一个编程模型：

$$y=a\ast (1-e^{-bx})$$

其中 x 是下拉的距离，y 是界面移动的距离，a 和 b 是常量，e 是自然对数的底数。这个公式的性质是，当 x 增大时，y 的增量会逐渐减小，即阻尼效果逐渐增大。当 x 足够大时，y 将接近于 a，即界面几乎不再移动。常数 a 决定了当 x 趋于 ∞ 时，y 的最大值；常数 b 决定了阻尼增加的速度。

这里将 a 和 b 都设置为 1，在 desmos 网站上，最终得到的图形如下：

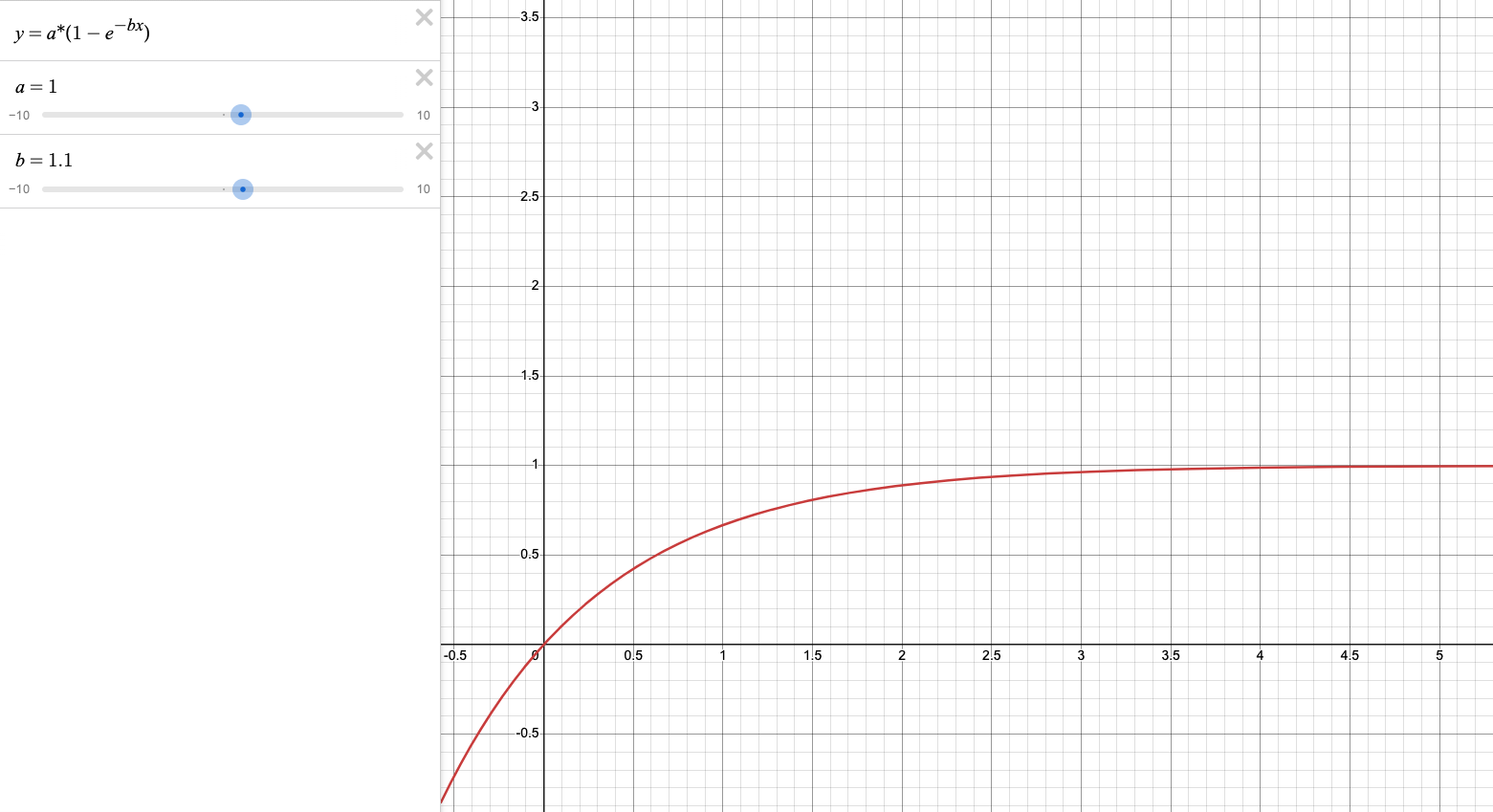
如果我们将常数 b 设置为更大一点，将会得到如下图形：

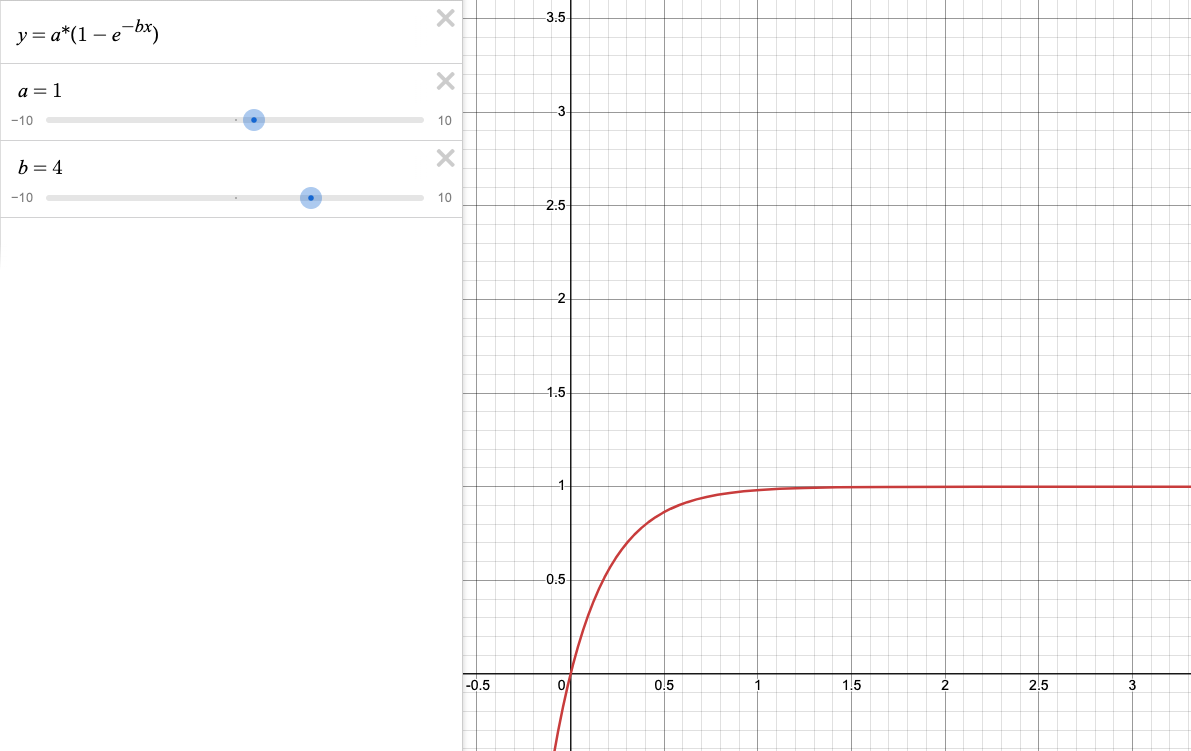
这个效果就比较符合我们想要的下拉阻尼效果，那么应该如何映射为可编程模型呢？

拖拽事件

这里以移动端 h5 为例，当下拉开始的时候，会触发 touchstart 事件，在持续拖拽的过程中，会触发 touchmove 事件。首先我们创建如下 div：

<div class="list">
    <div class="list-item"></div>
    <div class="list-item"></div>
    <div class="list-item"></div>
</div>

添加对应的样式：

.list {
    position: relative;
}

.list-item {
    height: 50px;
}

.list-item:nth-of-type(odd) {
    background-color: cadetblue;
}

.list-item:nth-of-type(even) {
    background-color: orange;
}

我们需要监听拖拽事件，然后应用阻尼数学模型，去动态设置列表的 top 值。这个阻尼效果，最直观的体现就是移动距离会越来越小，所以重点就是营造这种感觉。按照上面提到的公式，先进行参数的初始化：

const list = document.querySelector('.list')
const a = 50 // 当x趋于∞时，y的最大值
const b = 0.5 // 阻尼增加的速度
let startY = 0 // 记录触摸开始的位置

触摸开始的时候，需要在 touchstart 里进行记录：

list.addEventListener('touchstart', (event) => {
    startY = event.touches[0].clientY
})

我们核心是在 touchmove 事件函数里进行实时计算：

list.addEventListener('touchmove', (event) => {
    let distance = Math.max(0, event.touches[0].clientY - startY) // 计算下拉的距离
    let y = a * (1 - Math.exp(-distance * b))  // 利用公式计算阻尼效果
    list.style.top = `${y}px`
})

下面是浏览器模拟下拉效果：

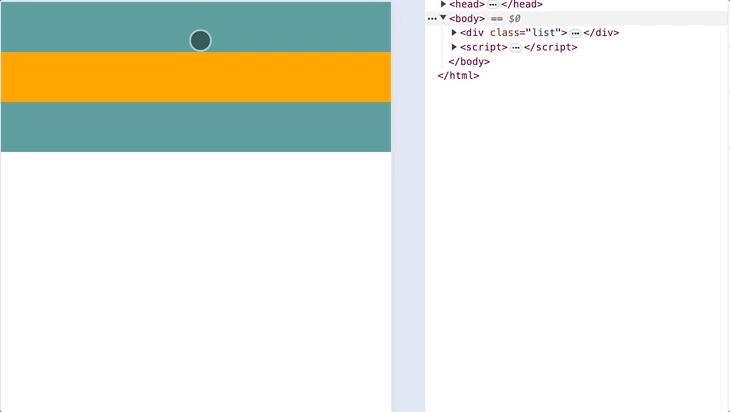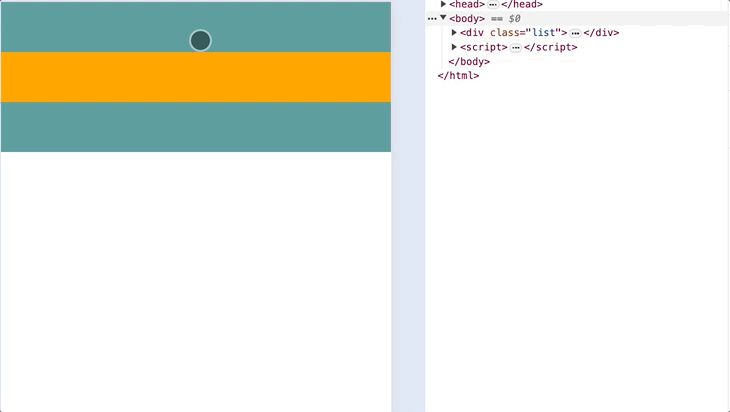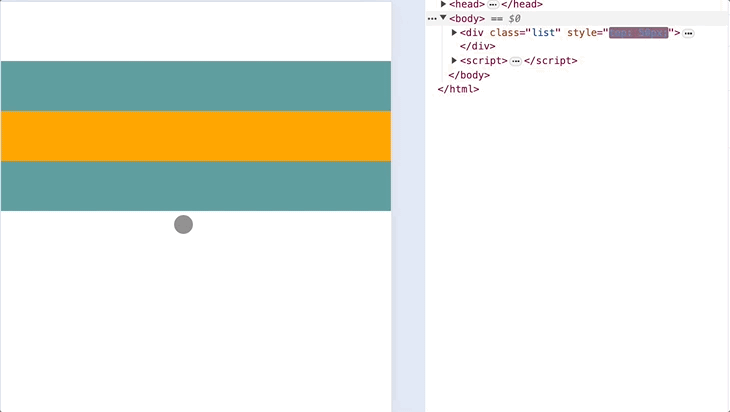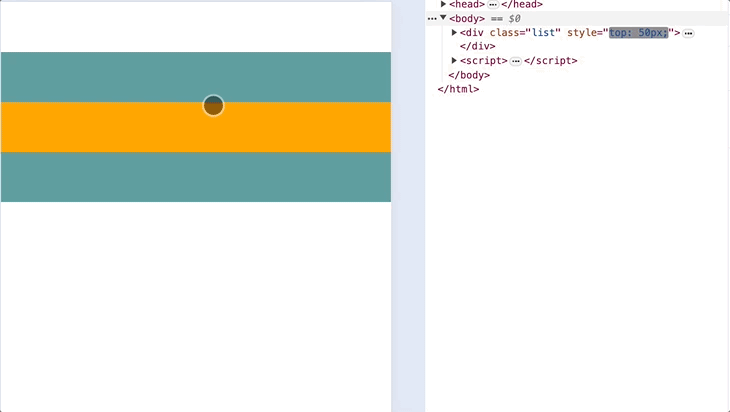
出现了一个很明显的问题，就是下拉的一瞬间，top 值发生了陡增，立马变为了 50px，显然这不符合预期。因为 a 值过大，所以我们需要调整参数 b：

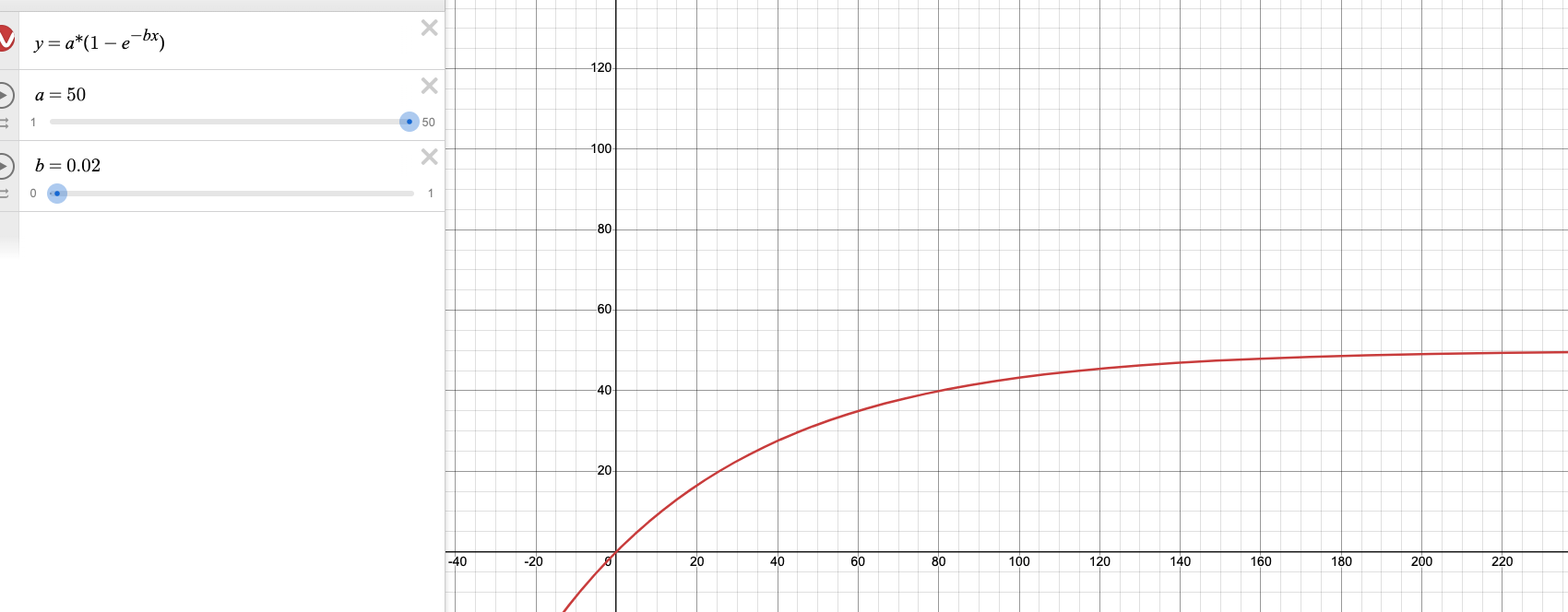
重新设置参数 a 和 b 之后，在浏览器模拟下拉效果如下：

为了在真机上测试，需要先阻止掉浏览器默认事件（比如触发浏览器下拉刷新），在真机上的效果如下：

回弹

回弹的效果和阻尼效果是相反的，即阻尼效果越大的时候，对应的回弹效果越明显，物体的移动速度就越快。可以通过建立模型，得到一个类似的数学公式，但是为了简单起见，这里回弹效果使用了 CSS。

list.addEventListener('touchend', (event) => {
    event.preventDefault()
    list.style.transition = 'top 0.3s'  // 恢复过渡效果
    list.style.top = 0 // 恢复原位
})

因为下拉阻尼是通过编程实现的，所以在开始下拉时，需要清除 CSS 缓动效果：

list.addEventListener('touchstart', (event) => {
    event.preventDefault()
    startY = event.touches[0].clientY
    list.style.transition = ''  // 清空过渡效果，使元素可以立即响应用户的操作
})

回弹模型

CSS 虽然能实现回弹效果，但是这里我还是希望先建立数学模型，然后倒推一个近似公式，去通过建立编程模型实现回弹效果。

以弹弓为例，当我们拉开弹弓，阻尼力会越来越大，直到达到一个最大值。此时，物体受到的力最大，同时物体质量恒定，其加速度最大。当我们松开手的一瞬间，随着阻尼力的减小，物体的加速度也会随之减小。由于阻尼力并非线性变化，因此物体的加速度也是非线形变化的，即先快后慢，直到最终的加速度为 0。

首先是有一个最大距离，其次是随着时间推移，加速度逐渐减小，直到趋于 0。用数学公式来描述如下：

$$y=a\ast e^{-bx}$$

和前面推导的阻尼近视公式相反，其对应的图像如下：

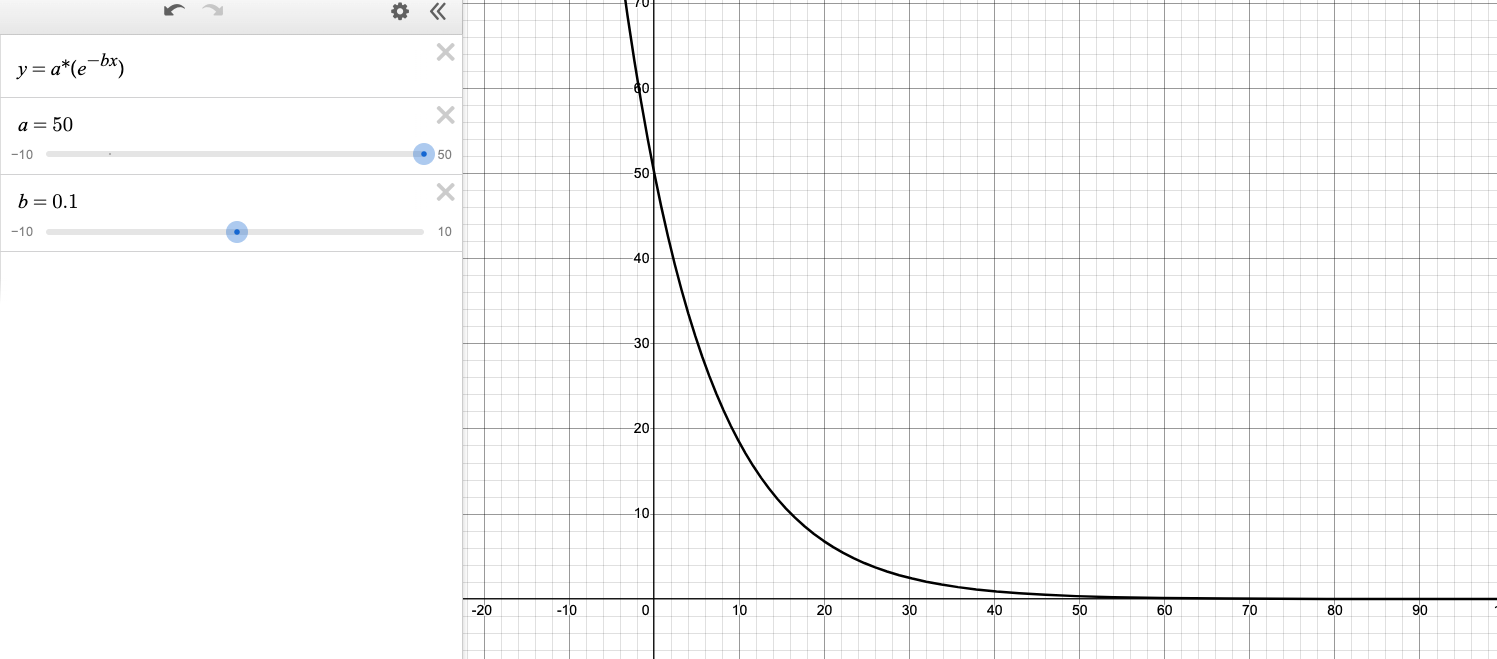
还是以上面的例子继续，我们把 CSS 动效都去掉，然后将回弹效果转换为代码：

list.addEventListener('touchend', (event) => {
    event.preventDefault()
    startY = list.getBoundingClientRect().top
    bounceBackId = requestAnimationFrame(bounceBack)
    // list.style.transition = 'top 0.3s'  // 恢复过渡效果
    // list.style.top = 0 // 恢复原位
})

const bounceBack = () => {
    const a2 = 50
    const b2 = 0.1

    let y = a2 * Math.exp(-startY * b2)
    y = Math.round(y)
    list.style.top = `${y}px`

    if (y) {  // 当 y 的绝对值等于 0 时，结束动画
        bounceBackId = requestAnimationFrame(bounceBack)
    } else {
        cancelAnimationFrame(bounceBackId)  // 结束动画
    }
}

编程模型

在上述例子中，我们依赖两个参数：常数 a 决定了当 x 趋于 ∞ 时，y 的最大值；常数 b 决定了阻尼增加的速度。如果下拉距离有所不同，对应的阻尼常数 b 也需要跟着调整。尤其是我们在封装一个下拉刷新组件的时候，不同场景下所设定的阈值不同，我们希望不用关注常数 b 就能自适应阻尼效果。

在回弹效果中，我们也是通过建立数学模型去计算的下一帧距离。使用数学公式可以直观地描述问题，但是在实际场景中，因为使用了 requestAnimationFrame，当 x 轴（时间）无限大时，如果常数 b 设置不正确，会触发大量计算，导致再次下拉的时候，RAF 还在计算，从而出现卡顿问题。

因此我们需要根据数学模型，建立一个有效的编程模型，才能解决这个问题。

阻尼编程模型

上文阻尼效果对应的图像，曲线是连续平滑的，x 值趋于无穷大的时候，y 值恒定，实际上我们可以简化这个过程。通过对距离进行分区段，在不同区段内设置不同的斜率，就能近似地实现这个效果。

这里推荐一个线形插值法函数 Lerp：

function lerp(start, end, factor) {
    return (1 - factor) * start + factor * end;
}

在这个函数中，start 和 end 是你想要过渡的两个值，factor 是一个介于 0~1 之间的数，表示过渡的比例。例如，如果 factor 是 0.1，那么返回的值将会更接近 start；如果 factor 是 0.9，那么返回的值将会更接近 end。

因此在 touchmove 事件监听函数里，我们需要实时计算可滚动距离：

list.addEventListener('touchmove', (event) => {
    event.preventDefault()
    start = lerp(start, end, factor)
    let y = maxDistance * start / end
    list.style.top = `${y}px`
})

回弹编程模型

同理，这类我直接贴上改造后的代码：

list.addEventListener('touchend', (event) => {
    event.preventDefault()
    startY = list.getBoundingClientRect().top
    start = 0
    bounceBackId = requestAnimationFrame(bounceBack)
})

function lerp(start, end, factor) { // 建议按照 start 为 0，end 为 100 来计算，便于实际运算时转换为百分比
    return (1 - factor) * start + factor * end
}

let start = 0
const end = 100
const factor = 0.2
const maxDistance = 50

const bounceBack = () => {
    start = lerp(start, end, factor)
    let y = maxDistance * (1 - start / end)
    list.style.top = `${y}px`

    if (Math.abs(end - start) > 0.01) {  // // 当前值和目标值足够接近时，停止更新
        bounceBackId = requestAnimationFrame(bounceBack)
    } else {
        cancelAnimationFrame(bounceBackId);  // 结束动画
        list.style.top = 0
    }
}

对应的效果如下：

完整 demo 代码

<!DOCTYPE html>
<html lang="en">
<head>
    <meta charset="UTF-8">
    <meta name="viewport" content="width=device-width, initial-scale=1.0">
    <title>Document</title>
    <style>
        body {
            margin: 0;
        }

        .list {
            position: relative;
        }

        .list-item {
            height: 50px;
        }

        .list-item:nth-of-type(odd) {
            background-color: cadetblue;
        }

        .list-item:nth-of-type(even) {
            background-color: orange;
        }
    </style>
</head>
<body>
    <div class="list">
        <div class="list-item"></div>
        <div class="list-item"></div>
        <div class="list-item"></div>
    </div>

    <script>
        const list = document.querySelector('.list')
        let startY = 0 // 记录触摸开始的位置
        let bounceBackId = null;
        let isDragging = false // 记录是否在进行拖动

        let start = 0
        const end = 100
        const factor = 0.1
        const maxDistance = 50 // 下拉最大距离
        const dragThreshold = 10 // 触发拖动的最小距离

        list.addEventListener('touchstart', (event) => {
            event.preventDefault()
            start = 0 // 重置 start，避免上一次下拉后 RAF 还在计算，导致瞬移
            startY = event.touches[0].clientY
            if (bounceBackId) {
                cancelAnimationFrame(bounceBackId)
                bounceBackId = null
            }
            isDragging = false
        })

        list.addEventListener('touchmove', (event) => {
            event.preventDefault()
            let distance = event.touches[0].clientY - startY
            if (Math.abs(distance) > dragThreshold) {
                isDragging = true // 检测到拖动
            }
            if (!isDragging) return
            start = lerp(start, end, factor)
            let y = maxDistance * start / end
            list.style.top = `${y}px`
        })

        list.addEventListener('touchend', (event) => {
            event.preventDefault()
            if (!isDragging) return
            start = 0 // 启动 lerp 函数，重置 start
            bounceBackId = requestAnimationFrame(bounceBack)
            isDragging = false
        })

        function lerp(start, end, factor) {
            return (1 - factor) * start + factor * end
        }

        const bounceBack = () => {
            start = lerp(start, end, factor)
            let y = maxDistance * (1 - start / end)
            list.style.top = `${y}px`

            if (Math.abs(end - start) > 0.01) {  // // 当前值和目标值足够接近时，停止更新
                bounceBackId = requestAnimationFrame(bounceBack)
            } else {
                cancelAnimationFrame(bounceBackId);  // 结束动画
                list.style.top = 0
                start = 0
                startY = 0
            }
        }
    </script>
</body>
</html>

参考文档

• cubic bezier
• desmos